Detail from the Hyperbolic Crochet Coral Reef. Photo Credit: NearEMPTiness, Wikimedia Commons.

Title Quote from The Holy Bible, Douay-Rheims Version, Ephesians 3:18

A recent podcast episode of On Being with Krista Tippett features a conversation with Margaret Wertheim, a science writer who is interested in making difficult scientific concepts more accessible to the public.  She joined forces with her identical twin sister Christine (who is an artist), and together they developed The Institute for Figuring (http://theiff.org).  Its mission is to explore ways of using the arts in order to visualize and “embody” challenging ideas found in science and mathematics.  An example of such a convergence comes from mathematician Dr. Daina Taimina– she discovered that hyperbolic geometry can be demonstrated by making crocheted surfaces, because with crochet you can build “frills” or “flounces” which follow different mathematical rules than the straight lines and flat surfaces that we are used to.

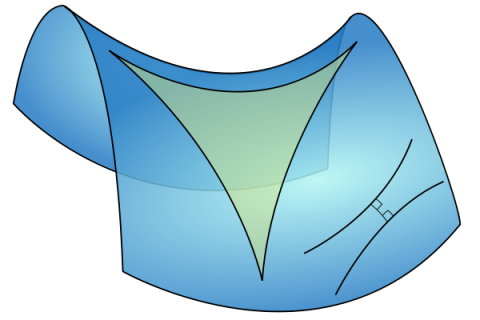
Hyperbolic Triangle.  Illustration from Wikimedia Commons.       Detail from Example of Hyperbolic

                                                                              Plane in Crochet.  Photo Credit: Durova, Wikimedia Commons.                                

The twin sisters developed Dr. Taimina’s techniques into an expansive project called the Crochet Coral Reef, which grew through the contributions of volunteers who crocheted various forms of sea creatures.  The incredible art exhibition that emerged shows us just how beautiful higher mathematics can be.

Detail from the Hyperbolic Crochet Coral Reef.  Photograph from Wikimedia Commons.

Crochet isn’t the only medium that allows a peek into higher mathematical concepts.  Mathematicians have long used origami to demonstrate geometry problems and find solutions by working through folded constructions.  Even two foundational geometry problems devised by the ancient Greeks (“doubling the cube” and “trisecting the angle”) cannot be solved using classical compass-and-straightedge methods but can be solved using origami.

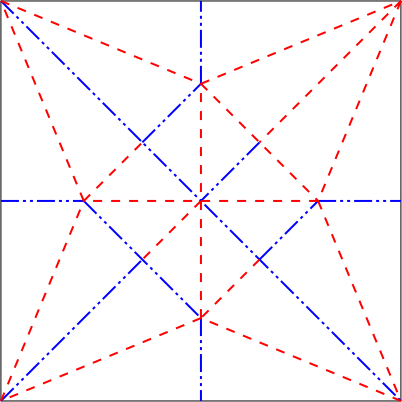
Origami Crease Pattern. Illustration Credit: Dmcq, Wikimedia Commons.

Exploring higher mathematics with handicrafts offers a glimpse of the more hidden or abstract characteristics of a space by being able to manipulate it in a (literally) “hands-on” way.  In the construction of these creations, mathematics can be seen brought to life– science and art stitched together, unfolding before our very eyes.

Origami Cranes at Phipps Conservatory and Botanical Gardens.  Photo Credit: Dllu, Wikimedia Commons.